认知偏差、贝叶斯和批判性思维
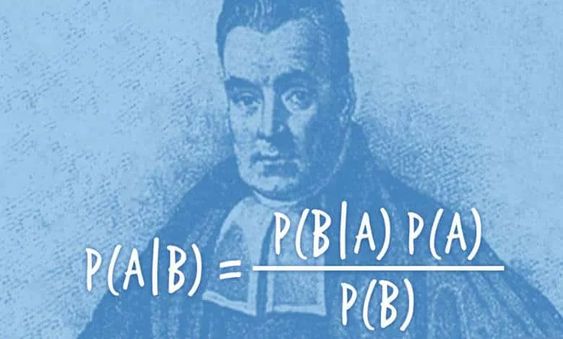
Summary
🎯 Weekly Sharing
认知偏差
由于最近在工作中犯了错误,而得到老板的批评。负面情绪使你觉得自己的错误不可宽恕,逐步放大自己的缺点,逐步加强的负面情绪充斥了你的整个生活从而产生了自我否定。
这种属于典型的近因偏差(Recency Bias),这种偏差会让人觉得最近比过去更重要,高估最近发生的事情对未来的影响。但实际正如下图,你觉得的不可饶恕的错误,可能正是你积攒能量继续向上的机会。
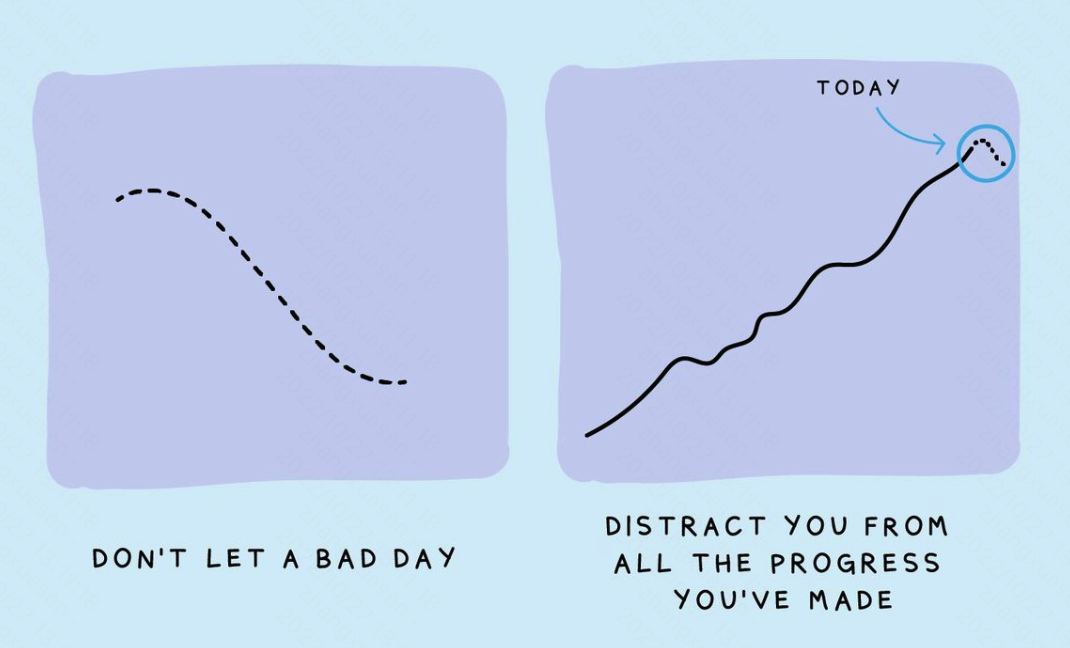
认知偏差(Cognitive bias),是指人们根据一定表现的现象或虚假的信息而对他人作出判断,从而出现判断失误。 认知偏差可导致判断不精准或各种统称「不理性」的结果。
有人总结了50种认知性偏差。理解认知偏差,有利于我们更好的认识自己和这个世界,从而做出更好的决策。
贝叶斯推理
贝叶斯推理可以表示为后验概率 = 先验概率 x 似然函数,公式如下:
\[\begin{aligned} P(H \mid E) \simeq P(E \mid H) * P(H) \end{aligned}\]其中H是假设、E是数据、P代表概率,P(H)代表先验概率、P(H|E)代表后验概率、P(E|H)是似然(实验数据)。简单来说,先验代表你对某件事情的猜测或者假设,后验代表你根据某些数据E推理出的结果。任何一个科学的推理过程,需要大量数据的支撑。
神奇的硬币
你某天出去散步,遇到了漂亮的仙女,仙女给你一枚神奇的硬币并说:“它抛出正面和反面的概率不相等,如果你能算出正确的概率分布,我就嫁给你”。假如你抛3次都是“正面”,你敢草草的得出结论“它抛正面的概率为1吗”,你可能不会,你知道这可能是运气,你想稳一点。
Beta分布
统计学上有一个很有意思的分布叫Beta分布,记为:
\[Beta(a,b)\]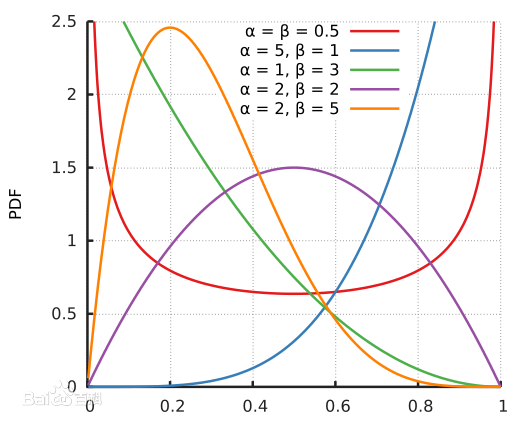
根据不同的$a,b$参数,Beta可以有不同的形态,很适合用来做先验分布。而且用Beta分布模拟扔硬币的先验分布后,通过贝叶斯推理,得到的后验分布依然是Beta分布。比如:
\[Beta(a,b) + 实验数据 = Beta(a + 正面,b + 反面)\]你对这枚硬币知之甚少,所以比较稳的方法是假设它是均匀分布的(也就是正反面概率都一致), $Beta(1,1)$能代表均匀分布。应用以上公式再具体到你的情况就是:
\[Beta(1,1) + (3,0) = Beta(4,1)\]其中(3,0)代表抛三次硬币3次多是正面。Beta分布对应的图像变化如下:
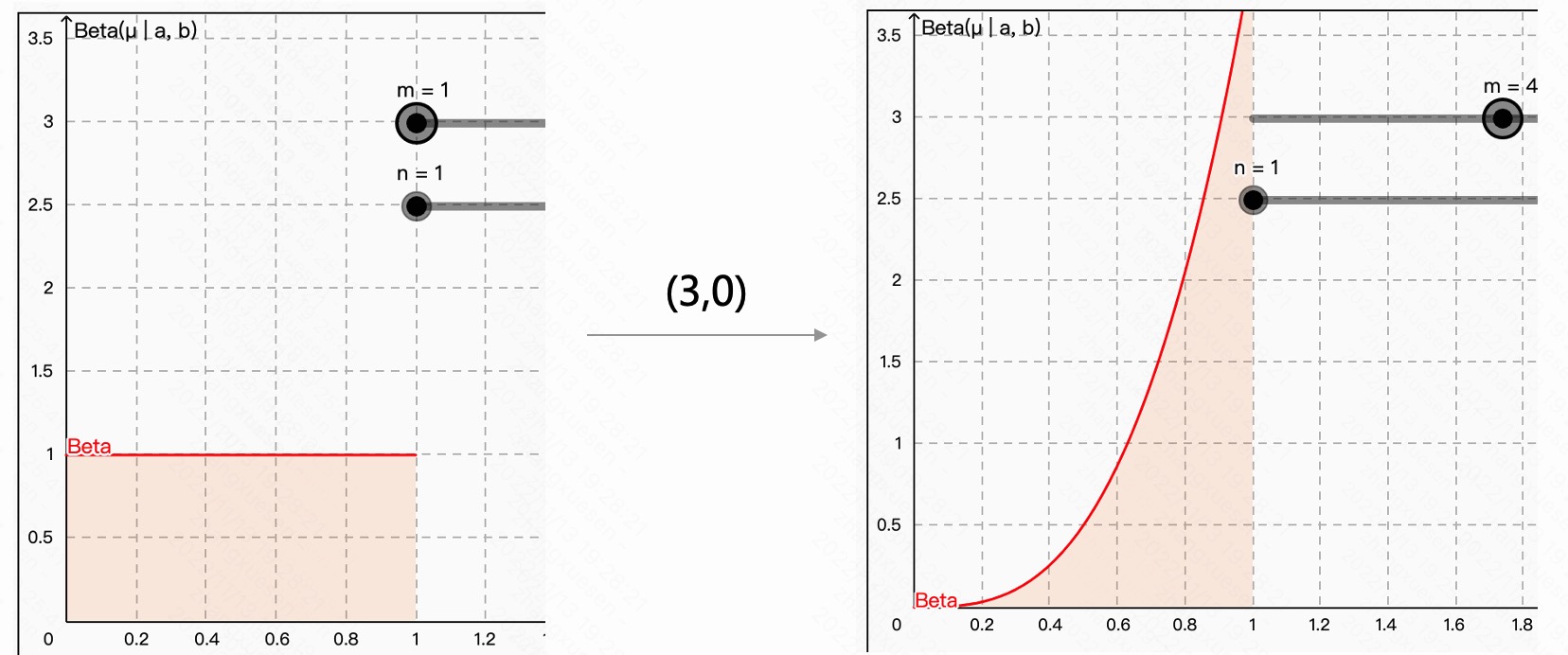
从图中可以发现,硬币抛出1的概率是很大的。随着你实验次数的变多,你可能最终会发现真实的概率。
不同的假设会有不同的结果
通过这枚硬币的研究,我们发现一个Beta分布的秘密(由于Beta分布的变化多端)。
- 相同的先验(假设) + 不同的(不充分的)观测数据,得到不同的后验(结论)
- 不同的先验(假设) + 相同的观测数据,也可以得到不同的后验(结论)
你突然想明白了,你是由于自己在工作上犯了错误(观测数据),然后做了错误的先验假设:自己很笨,最终才有了自我否定的心态(后验)。
这时候你想到了两种策略来缓和自己的负面情绪:
- 在“我笨”的先验下,我只是最近犯了一个错误,这个错误可能也具有运气不好的成分(随机性),我之前可是做了很多牛逼的事情呢,老板也经常夸我。 这样就得到了不一样的后验(我其实很聪明),你也在无形中破除了recentcy bias的影响。要想在一个假设下做出充分的论证,还需要大量的证据。
- 你改变了“我笨”的先验为“我其实很聪明”,然后这一个观测数据其实也就说明不了什么了,你会继续努力工作,然后通过“自证预言”式的自我激励完成“我聪明”的论证。
批判性思维
批判性思维(Critical Thinking)是人的思维发展的高级形式,它要求我们不要全盘接受某些观点,而是批判性的借鉴和吸收。
批判性思维的核心是质疑(提问)。不仅要去质疑结论,还要去质疑假设和证据。核心着眼于对方论证的整个过程(推理过程)而不是结论。
比如开篇的例子,我们不仅要去质疑导致“自我否定”的结论,还要去质疑”我很笨“的假设,也要去质疑是否”老板的一次批评“这个证据是否充分,就像上边提到的贝叶斯推理一样。
批判性思维,是一种思维方式,有了这个思维模型,我们在生活中能更好的认识自己和世界,更不为外界环境所左右。
但是切记,批判性思维是思辨,而不是为自己开脱和抬杠。即使是最优秀的批判性思考者有时也会犯错,犯错并不可怕,接受犯错就是进步的开始。
—— 💌 感谢你的阅读 ——
点个订阅